┘

In de exameneisen zit een merkwaardige ‘twist’:
De kandidaat hoeft het begrip ω, zijnde de cirkelfrequentie in rad/s, niet te kennen.
Maar de EJiG’s willen wel mooie ronde getallen.
Daarom behelpen ze zich met:  2∙π∙f = 2.105 rad/s.

Nu komt de kandidaat in de verleiding om ω (die ze niet snappen) om te rekenen naar f in Hz.
NIET doen!
Met ω heb je wel mooie getallen en veel formules worden ook eenvoudiger, b.v.
XL = ω∙L  of  ω = 1/√(L∙C) .

We gaan rekenen: 
XL = 2.105 x 20.10 ̶ 6 = 4 Ω.
Maar R = 4 Ω.
Nu kom je in de verleiding om te denken dat de bronspanning zich in gelijke stukken verdeelt.
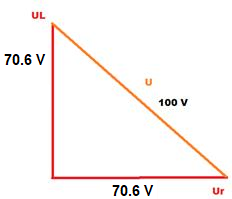
Teken het vectordiagram en constateer dat :

Z = √ 42 + 42 =   5.66 Ohm
I = U / Z = 100 / 5.6  = 17.66 A
Ur = Ir x R  =   17.66   x   4  = 70.6 V
Ul = IL x Xl =   17.66   x   4  = 70.6 V

U=100 V slaat op de diagonaal van een vierkant.
De rechthoekzijden (UL & UR) zijn beide ≈ 70,7 V
(antwoord A).



Merk op dat ik ONGEMERKT gebruikmaak van een handige eigenschap van het vectordiagram van de serieschakeling:
De impedantie-figuur is GELIJKVORMIG met de spanningsfiguur.
Als in de impedantie-figuur geldt
Rechthoek zijde² x  Rechthoek zijde²  = Schuine zijde² ,
geldt dat OOK in de spanningsfiguur.