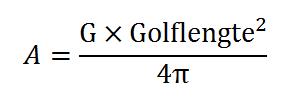┘
Stel je het volgende voor:
Een zendantenne zendt een vermogen uit van 1 Watt, en het vermogen verspreidt zich bolvormig (dus alle kanten op) van de antenne vandaan.
De antenne is in dit geval dus isotroop.
Dat betekent dat als we wat verder weg zitten, het bol oppervlak inmiddels behoorlijk groot is geworden.
Die ene Watt vermogen is dan verspreid over die gehele bol.
Hoe verder weg je staat, hoe 'dunner' de vermogensconcentratie op het oppervlak van een bol. Immers, die ene Watt wordt over een steeds groter boloppervlak verspreid.
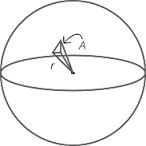
Stel je hebt een dipool antenne en daar ga je mee ontvangen.
Als dat signaal langs komt (de bol passeert je als het ware), dan 'hapt' de antenne er een beetje vermogen uit en wordt er spanning in je antenne opgewekt.
Nu geldt: hoe langer de antenne, hoe meer vermogen er uit de bol wordt gehapt.
Je kunt dit uiteindelijk uitdrukken in een hoeveel vierkante meter van het boloppervlak waarvan je het vermogen eruit hapt met je antenne.
Dat is dan in de tekening het oppervlak A.
Als nu de totale oppervlakte van de bol gelijk aan A(bol) is, dan pak je met je dipool als het ware aan vermogen op:
De verhouding tussen het 'oppervlak van de antenne' en de oppervlakte van de bol x 1 Watt
(een heel klein deel van die ene Watt zendvermogen dus) is wat de antenne aan vermogen 'hapt'.
Hoe verder je weg zit van de zender, hoe groter het boloppervlak is en dus hoe minder vermogen per vierkante meter boloppervlak beschikbaar is.
De oppervlakte A(antenne) wordt ook wel de effectieve oppervlakte van de antenne genoemd.
Deze effectieve oppervlakte wordt berekend met de formule:
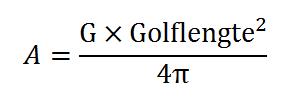
Let op: Golflengte in het kwadraat !!! (examen vraag)
Hier is G de gain van een dipool t.o.v. de isotrope antenne: factor 1,64 (dit is een gain van 2,15 dB van de dipool t.o.v. de isotrope straler) en verder is er de golflengte die je gebruikt in het kwadraat gedeeld door het getal 4 x pi.
Als je dit uitrekent voor de dipool, dan krijg je 1,64 / 4 pi x de golflengte in kwadraat = 0,13 x golflengte in kwadraat.
De effectieve oppervlakte van een dipool 20 m dipool wordt dan 0,13 x 20 x 20 = 52 vierkante meter.
Van een 40 m dipool wordt dat dan 0,13 x 40 x 40 = 208 vierkante meter.
Je ziet nu meteen: hoe langer de golflengte, en hoe langer de dipool (die een halve golflente lang is), hoe meer vermogen je uit de lucht 'hapt'.
Dat is dan het vermogen dat beschikbaar is voor de ingang van je ontvanger.
Een eenvoudige manier om het effectieve oppervlak van een dipool te onthouden is het volgende.
De lengte van de dipool is 0,5 x de golflengte.
Ondanks dat het draadje van de dipool vrij dun is t.o.v. de golflengte trekt hij het vermogen uit de lucht dat tot ongeveer 1/8 golflengte afstand van de draad nog langskomt.
Aan beide zijden is dat dan opgeteld 1/8 + 1/8 = 1/4 golflengte.
Het totale oppervlakte is dan lengte x breedte = 0,5 golflengte x 0,25 golflengte = 0,125 x golflengte^2, oftewel afgerond ongeveer 0,13 golflengte in het kwadraat.
Dit betekent bijvoorbeeld dat een dipool voor 70 cm minder vermogen uit de lucht hapt dan een dipool voor 2 meter.
De golflente voor 2 meter is 3 keer zo lang, en dat betekent dat een 2 meter dipool (golflengte = 2 meter) 9 keer zoveel vermogen uit de lucht hapt dan een 70 cm dipool (golflengte 70 cm).
Dit gaat om een factor 9 in vermogen!
Als je die factor van 9 keer vermogen omrekent naar spanning, dat betekent dan dat een 2 meter dipool 3 keer zoveel spanning maakt voor de ontvanger als die van 70 cm (als zendvermogen en afstand gelijk blijven).
Je zou kunnen bedenken dat hoe korter de golflengte, hoe minder goede ontvangst je hebt.
En ja, dat is waar. Gelukkig kun je nog iets aan de gain van de antenne doen, die staat ook in de formule.
Gelukkig is dan een 20 elements 70 cm Yagi met veel gain niet zo groot en kun je die nog met een rotor draaien
(probeer dat maar eens met een 20 elements beam voor de 20 m band).
De grote schotels richting het heelal (satellietcommunicatie) werken met centimeter golven en hebben een hele grote gain.
Hoe groter de schotel, hoe hoger de gain.
Tegelijk: hoe groter de schotel hoe groter de effectieve oppervlakte, zowel fysiek als in de bovenstaande formule.
Denk eens over het volgende na:
->De effectieve oppervlakte (volgens de formule) van een schotelantenne ligt ongeveer tussen de 50 en 70% van de fysieke grootte.
Dus geldt bij gelijkblijvende ontvang-golflengte: hoe groter de schotel, hoe meer gain en hoe meer effectieve oppervlakte.
Fysieke oppervlakte en de bovengenoemde uitgerekende effectieve oppervlakte 'lopen met elkaar mee'.
->Stel we houden dezelfde schotel maar ontvangen een wat kleinere ontvang golflengte.
Er wordt dan bij benadering net zoveel vermogen uit de lucht gehapt.
Dat komt puur doordat de fysieke schotel oppervlakte niet verandert.
In de formule compenseert de toegenomen gain van de schotel de lagere waarde van golflengte in het kwadraat, zodat in dit geval de
effectieve oppervlakte ongeveer gelijk blijft.