┘
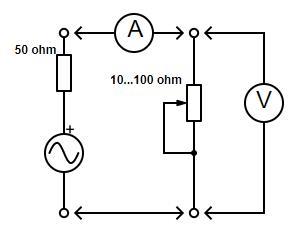
Een spanningsbron heeft een zekere inwendige weerstand.
We kunnen ons nu de vraag stellen hoe groot de aangesloten weerstand zal moeten zijn om een maximale vermogensoverdracht te verkrijgen.
De spanningsbron en de inwendige weerstand vormen samen een niet ideale spanningsbron.
Als in bovenstaand schema de stroom en de spanning maximaal zijn, vindt de maximale vermogensoverdracht plaats.
We kunnen een staatje maken met daarin de waardes van de stroom en spanning bij verschillende waardes van de instelbare weerstand.
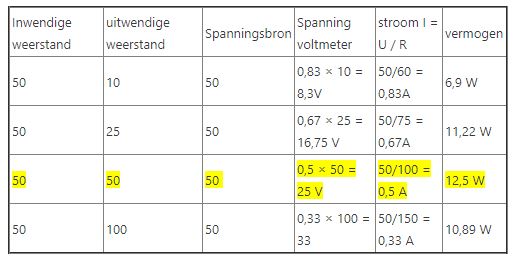
De stroom rekenden wij uit door de inwendige en uitwendige weerstand bij elkaar op te tellen en te zien over de spanningsbron.
Bij 10 Ohm uitwendige weerstand: 50 Ohm (inwendig) + 10 Ohm (uitwendig) = 60 Ohm.
De spanning hebben wij in de tabel gesteld op 50 Volt.
De stroom zal dan zijn I = UR=5060 = 0,83 A.
De spanning over de uitwendige weerstand is dan U = I × R = 0,83 × 10 = 8,3 Volt.
Het vermogen is dan P = I × U = 0,83 × 8,3 = 6,9 Watt.
Ditzelfde is gedaan bij een uitwendige weerstand van 25, 50 en 100 Ohm.
In de rechter kolom zien we het opgenomen vermogen en we zien dat de maximale vermogensoverdracht plaatsvindt als de uitwendige weerstand gelijk is aan de inwendige weerstand, 50 Ohm in dit geval.
Nu is 50 Ohm een vrij hoge inwendige weerstand, maar uitgangen van eindtrappen van zenders hebben vaak deze inwendige weerstand.
Je zult nu begrijpen als we een coaxkabel en antenne van 50 Ohm aansluiten, de vermogensoverdracht het grootst zal zijn.
Als de inwendige weerstand gelijk is aan de uitwendige weerstand zal de vermogensoverdracht het grootst zijn.