┘
Digitale modulatie is het overbrengen van informatie door middel van ééntjes en nulletjes.
Sinds de komst van de pc in de jaren 80 van de 20e eeuw zijn er steeds meer en meer radio-amateurs gaan experimenteren met digitale communicatie. Hoewel CW ook het principe heeft van ééntjes en nulletjes, en in feiten ook digitaal is, behandelen wij hier moderne digitale modulatievormen.
Er zijn op dit moment, 2016, meer dan honderd verschillende digitale modulatievormen. RTTY, PSK en JT65, FT8 zijn op dit moment het meest gebruikt.
Digitale modulatie is een digitaal signaal op een analoge draaggolf.
De computer wordt aangesloten op de tranceiver en de computer maakt er wat van.
Meestal zal de informatie uit leestekens bestaan.
Tegenwoordig wordt ook spraak digitaal overgebracht via sommige systemen zoals D-star en DMR, maar de bewerking van het digitale signaal vindt hier plaats in het apparaat zelf.
Ook de omroep zendt tegenwoordig digitaal uit, zo is de opvolger van FM in omroepland DAB+.
Dit is ook een analoog signaal dat digitaal gemoduleerd wordt, maar meestal in de ontvanger zelf al verwerkt wordt tot bruikbare informatie.
RTTY, PSK en JT65 wordt (vooralsnog) door de computer verwerkt.
Ze werken op basis van frequentieverschuiving of faseverschuiving.
FSK
Frequentie shift keying.
Hierbij verschuift de frequentie van de draaggolf, het is een vorm van frequentiemodulatie.
Omdat we slechts met enen en nullen werken, zijn er maar 2 frequenties nodig.
Eén frequentie staat voor nul, meestal de center frequentie, de andere frequentie staat voor één.
De frequenties liggen standaard 170 Hz uit elkaar.
Het verschil tussen de centerfrequentie en de 170 Hz hoger of lager liggende frequentie noemen wij de shift.
De frequentie van de draaggolf verandert hier.
AFSK
Dit werkt bijna volgens hetzelfde principe van FSK, alleen wordt hier door middel van een audiosignaal een toon uitgezonden als een AM, SSB of FM signaal.
Deze toon laten we een klein beetje variëren tussen bijvoorbeeld 1000 en 1100 Hz.
De 1000 Hz staat dan voor de nul en de 1100 Hz voor de een.
2-PSK en 4-PSK
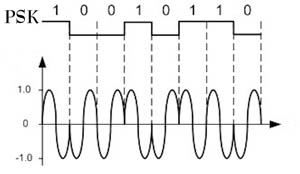
Van PSK heb je misschien wel eens gehoord, het staat voor Phase Shift Keying.
Anders dan bij FSK waarbij de frequentie variëert tussen 2 punten, is het bij 2-PSK zo dat de fase wisselt tussen 2 punten.
Een fase kan bijvoorbeeld bij 0 graden een 1 voorstellen en bij 180 graden een 0.
Boven zie je bij het wisselen van het symbool van 0 naar 1 de fase verspringt.
In plaats van dat de sinus doorloopt naar beneden, gaat hij meteen weer omhoog.
Dit houdt in dat de fase 180° gedraaid is.
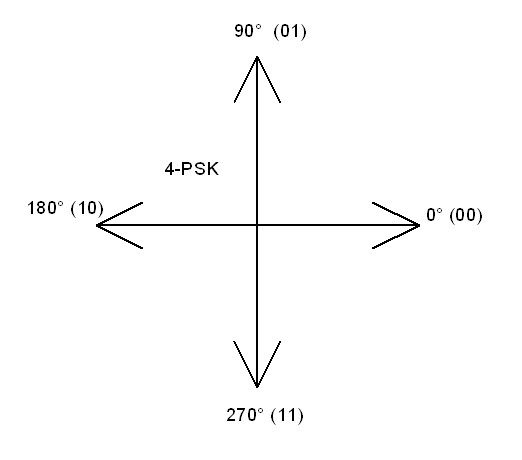
4 psk
Bij 4-PSK varieert de waarde tussen 4 punten, tussen 0°, 90°, 180° en 270°.
Omdat we maar 2 waardes nodig hebben bij een digitaal signaal, kunnen we 4 keer per periode een 0 of een 1 uitzenden.
4-PSK is daardoor 2 keer sneller dan 2-PSK.
Zo kunnen wij in plaats van op 4 punten in de sinus de fase draaien, ook bijvoorbeeld na elke 5 graden de fase laten draaien, men heeft dan 72 punten waar de fase kan draaien.
QAM
Naast het draaien van de fase is er nog een manier om een digitaal signaal over te brengen, namelijk door de amplitude te veranderen.
Zo kunnen we bijvoorbeeld aan een amplitude van een ½ de waarde 0 hangen en aan een amplitude met volledige uitslag een 1.
Hierdoor heb je 2 keer zoveel mogelijkheden.
Als wij de fase draaien en de amplitude ook gebruiken voor de modulatie, spreken wij van QAM.
Wij noemen dit multi-level codering.
Als we faseverschillen gebruiken van 45° en 2 verschillende amplituden, dan hebben wij QAM-16.
We hebben 8 punten in de faseverschillen, maar die kunnen ieder weer de amplitude 1 of 2 hebben, we hebben 16 mogelijkheden.
In de digitale televisie wereld wordt meestal 256 QAM gebruikt, dit houdt in dat er zeer kleine fasehoeken kunnen worden gedetecteerd.
Hiervoor is veel rekenkracht nodig en een stabiel ongestoord signaal. 256 QAM is dan ook niet zo geschikt om via de ether uit te zenden, maar via een gesloten kabelnetwerk kan het prima werken.
Voor digitale amateurtelevisie zullen we teruggrijpen naar een lagere multi-level codering.
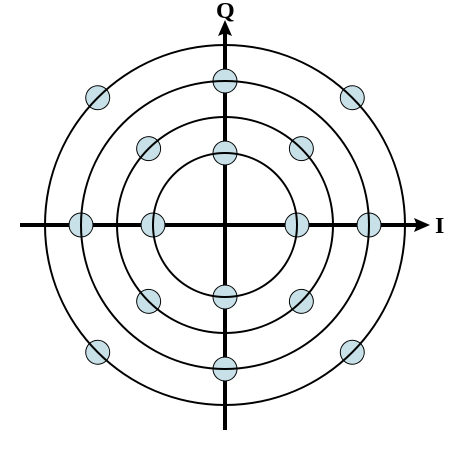
Hierboven zie je een voorbeeld van 16 QAM, er zijn 16 verschillende punten waar de waarde kan worden gedetecteerd.
Als je kijkt op 45 graden zie je dat de amplitude 2 waardes kan hebben, op 180 graden idem dito.
Op 0, 45, 90, 135, 180, 225, 270 of 315 graden kan de amplitude 2 waardes hebben.
Omdat we slechts met 2 waardes werken in de digitale techniek, de één en de nul, kunnen we berekenen hoeveel bits een symbool bevat bij 16 QAM.
Hoe vaak moeten wij 2 met zichzelf vermenigvuldigen om 16 te krijgen?
2 × 2 × 2 × 2 = 16. Dat is 4 keer. Het aantal bits per symbool is dan 4 bits.
1001 is een 4 bits symbool en het kan 16 waardes vertegenwoordigen van 0 tot en met 15.
Zie verder terug in hoofdstuk 1.7 van de N-cursus.
Bitsnelheid, symboolsnelheid en bandbreedte
Een digitaal signaal doet er een bepaalde tijd over om overgebracht te worden.
De snelheid waarmee dit gaat noemen wij bits per seconde.
De symboolsnelheid wordt ook wel baudsnelheid genoemd.
Alleen bij 1 bit, aan of uit, is 1 Baud gelijk aan 1 bit/s.
Baud wordt afgekort met Bd.
Om een symbool over te kunnen zenden zijn bijvoorbeeld 6 bits nodig, en de tijd dat het duurt dat een bit is overgezonden duurt bijvoorbeeld 25 ms, dan neemt het symbool 6 × 25 ms = 150 ms in beslag.
De symboolsnelheid, uitgedrukt in Baud, is dan 10,15 = 6,67 Bd
Baud is het aantal symbolen per seconde.
De duur dat een symbool nodig heeft is het aantal bits van het symbool maal de tijd dat een bit nodig heeft om overgezonden te worden.
1 (seconde) gedeeld door de (bit duur × aantal bits) is de symboolsnelheid in Baud.
Een bit heeft een bepaalde tijd nodig om overgezonden te worden
Symbool duurt deze tijd maal het aantal bits
Een baud is het aantal symbolen per seconde
Baud = 1 gedeeld door de symboolduur
Symboolduur = bitduur × aantal bits
Als we een bitduur zouden hebben van 200 ms, en we hebben een symbool van 8 bits, wat is dan de symboolsnelheid in Baud?
Oplossing:
Symboolduur is 200 ms × 8 bits maakt 1600 ms, oftewel 1,6 seconde
Symboolsnelheid is 1 gedeeld door de symboolduur is 11,6 = 0,625 Baud
Bandbreedte (bij digitale signalen)
Hoe hoger de snelheid is waarmee wij onze bits versturen, des te groter zal de bandbreedte worden. Als wij met 31 bits per seconde informatie zouden overbrengen, zou er elke 31 Hertz een zijband ontstaan, zowel boven als onder de zendfrequentie. Het aantal veelvouden van de zijbanden hangt samen met de snelheid waarmee de pulsen zijn opgebouwd. Is de tijd dat een puls opkomt oneindig klein, dan zal het aantal zijbanden oneindig groot zijn. De tijd dat een puls opkomt noemen wij de stijgsnelheid.
Om deze hoeveelheid zijbanden te voorkomen moet de stijgtijd wat langer duren, de puls moet rustig worden opgebouwd. Hoe langer de stijgtijd, of risetime, des te minder zijbanden er zullen zijn.
In de moderne digitale technieken is de bandbreedte beperkt tot soms niet meer dan 9 Hertz. In het populaire psk31 is de bandbreedte 31,25 Hz aan weerszijde van de uitzendfrequentie.



