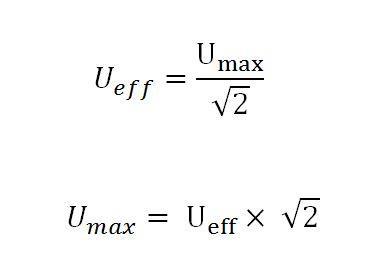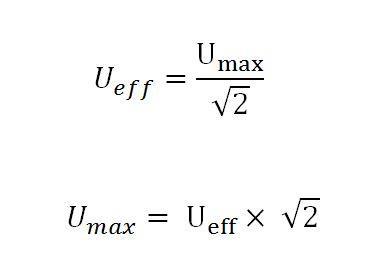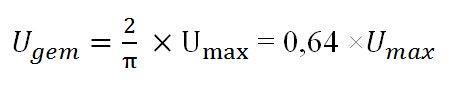┘
Een groot deel van deze les hebben wij al behandeld in de N cursus, heb je dit niet helemaal meer paraat, lees dan dit hoofdstuk in de N cursus nog eens door.
Momentele waarde
De momentele waarde van een sinus is de spanning op een bepaald moment in de tijd.
Als je bijvoorbeeld een sinus hebt die er 50 ms over doet om 2 keer door de 0 te gaan, dan is de waarde na bijvoorbeeld 3ms, 8ms, 37ms een momentele waarde.
Het berekenen van de momentele waarde valt buiten het bestek van deze cursus.
Wat je wel moet weten is dat de maximale momentele waarde de amplitude is.
Effectieve Waarde
Als je wel eens een stereo-audioversterker hebt gekocht zal het je wel zijn opgevallen dat het vermogen dat deze versterkers leveren in de duurdere klasse lager lijkt te zijn.
Dit is in werkelijkheid niet zo, maar is een verkooptrucje.
Men gaat er vanuit dat goedkope versterkers het beste verkopen als er meer Watts uitkomen, bij duurdere versterkers gaat men er van uit dat er meer gekeken wordt naar andere eigenschappen.
Bij goedkopere versterkers geeft men meestal het maximale vermogen aan, bij de betere versterkers de effectieve waarde.
Misschien heb je wel eens gehoord van RMS (root-mean-square), dit is het effectieve vermogen, het echt bruikbare vermogen.
De effectieve waarde van een sinus is de daadwerkelijk bruikbare waarde.
De maximale spanning uit ons stopcontact, of eigenlijk moeten we zeggen wandcontactdoos, is 324 Volt.
Nu zul je zeggen dat het niet klopt, want de spanning is 230 Volt.
Toch klopt het, de 230 Volt is de effectieve waarde en is net zo effectief als 230 Volt gelijkspanning.
De effectieve waarde is 0,707 maal de maximale waarde.
Als je van de effectieve waarde de maximale waarde wilt weten dan vermenigvuldig je deze met 1,41 oftewel met wortel 2.
Hieronder zie je dit in formulevorm.
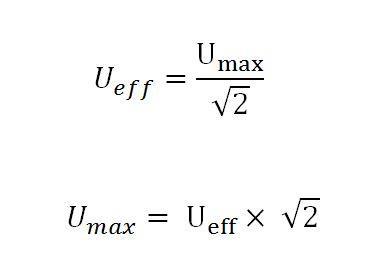
Gemiddelde waarde
Anders dan de effectieve waarde is de gemiddelde waarde.
Als we een volledige sinus voor ogen zien is de amplitude boven de nul gelijk aan de amplitude onder de nul, de gemiddelde waarde zal dan nul zijn. Nemen we nu alleen het gedeelte boven de nullijn, dan zal de gemiddelde waarde 2/Π × Umax zijn.
Deze formule geldt alleen voor een halve sinus.
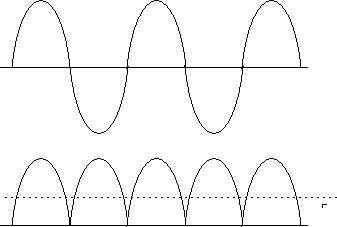
Dit komt van pas als we de sinus gaan gelijkrichten, we gaan dan de onderste helft van de sinus naar boven brengen.
Op het plaatje hierboven zie je boven de hele sinus, de onderkant heft de bovenkant op zodat men gemiddeld op 0 uitkomt.
Daaronder staat de dubbelfase gelijkgerichte sinus.
Nu heffen de twee helften elkaar niet op, maar
Over de periode, periodeduur, frequentie en de eenheid Hertz lees je in de N cursus.
Faseverschil
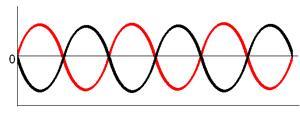
Als je twee golven hebt met dezelfde frequentie, en ze gaan op hetzelfde moment door nul, en beide zijn op hetzelfde moment negatief en positief , dan zeggen we dat de twee golven in fase zijn, ze versterken elkaar.
Als de 2 golven wel tegelijkertijd door de nul gaan, maar de een is positief terwijl de andere negatief is, dan spreken we van tegenfase. boven zie je 2 golven, een rode en een zwarte.
Als de rode positief is, is de zwarte negatief en andersom.
In deze tekening heffen ze elkaar helemaal op.
We haalden al eerder in de cursus een voorbeeldje uit de audiowereld aan, laagfrequent-golven hebben veel gemeen met hoogfrequent-golven, zeker wat betreft theorie.
Een voorbeeld van tegenfase in de audiowereld ken je misschien wel.
Als je de ene luidspreker goed aansluit, met de rode draad in de rode aansluiting op de versterker, maar de andere verkeerd, met de zwarte draad in de rode aansluiting, dan staan je luidsprekers in tegenfase.
Vooral de lage tonen doven elkaar uit en het stereobeeld is nogal merkwaardig.
Dit komt omdat de golven elkaar tegenwerken.
Je zal bij muziek nooit hebben dat je niets meer zult horen, omdat muziek niet 1 of 2 sinussen zijn maar een heleboel sinussen door elkaar.
Zet je nu een testtoon op de versterker van bijvoorbeeld 1000 Hertz, dan zal, als je een goede installatie gebruikt met identieke luidsprekers, op een bepaald punt tussen de luidsprekers nog maar weinig te horen zijn.
In theorie zou er niets te horen moeten zijn, maar dat kan met onze 2 oren niet, er is namelijk afstand tussen onze oren.
Als aan het linkeroor de golven precies uit fase zijn, is dat bij het rechteroor niet zo.
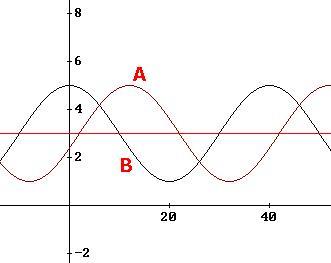
Meestal is het niet zo dat golven precies in fase of tegenfase staan.
Meestal staan de golven maar voor een deel uit fase en gaan ze niet tegelijkertijd door nul.
Boven zie je hier een voorbeeld van.
Er is een faseverschil en je kunt uit de tekening opmaken dat het ene moment golf A golf B versterkt terwijl op het andere moment de golf A golf B tegenwerkt.
Als we golf A als referentie nemen, zien we dat deze bij ongeveer 15 tijdseenheden maximaal is.
We zien dat golf B ongeveer bij 0 maximaal is.
Golf B loopt voor op golf A, we zeggen dan dat B voorijlt op A. Golf A kan bijvoorbeeld de spanning zijn, terwijl golf B de stroom is.
We zeggen dan dat de stroom voor-ijlt op de spanning.
Voor-ijlen en na-ijlen komen we vooral in deze cursus tegen bij condensatoren en spoelen en netwerkjes daarmee. In een spoel ijlt de spanning voor op de stroom.
Eerst komt de spanning en dan hobbelt de stroom erachteraan.
Bij een condensator ijlt de stroom voor op de spanning, eerst loopt de stroom en dan komt de spanning pas.
LUI en CIU
De L staat voor spoel, de U voor spanning, de I voor stroom en de C voor condensator.
Als je LUI onthoudt als je met na-en voor-ijlen te maken krijgt ben je al een heel eind.
LUI staat voor Spoel-Spanning-Stroom.
Bij een spoel is er eerst de spanning, de stroom ijlt na.
Bij een condensator is het precies andersom, die hoef je niet te onthouden, als je LUI onthoudt weet je dat een condensator CIU is. (eerst de stroom, dan de spanning).
Graden
Een golf, of eigenlijk horen wij van sinus te spreken, is onderverdeeld in graden zoals in een cirkel.
Het voorbeeldje hierboven laat je een hele sinus zien, het maakt inzichtelijk hoe de sinus in graden is opgebouwd.
Als de sinus maximaal positief is, is deze 90 graden, is deze maximaal negatief, dan is deze 270 graden.
Bij 0, 180 en 360 graden gaat deze door de nul.
0 en 360 graden is hetzelfde punt.
positief maximaal 90°
negatief maximaal 270°
nul bij 0° - 180° - 360°
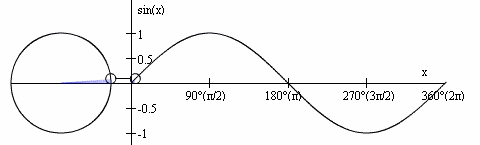
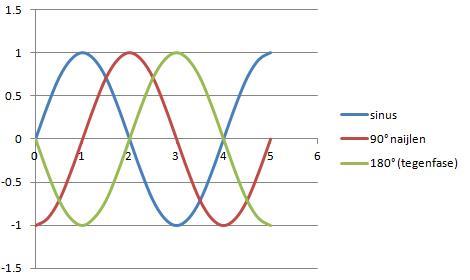
Hierboven zie je in blauw de sinus.
Bij 1 op de X-as hebben wij de 90 graden bereikt, bij 2 de 180 graden, bij 3 de 270 graden en bij 4 de 360 graden, die weer gelijk is aan 0 graden.
De rode lijn ijlt 90 graden na, bij 1 op de X-as heeft de blauwe sinus de 90 graden bereikt, terwijl de rode lijn dan nog maar op 0 graden zit, een faseverschil van 90 graden.
De groene lijn is totaal in tegenfase met de blauwe lijn.
Waar bij 1 de blauwe lijn zich op 90° bevindt, bevindt de groene lijn zich op 270°.
De lijnen zijn elkaars tegengestelden en zullen elkaar tegenwerken..
De rode lijn ijlt 90 graden na op de blauwe lijn, de groene lijn ijlt niet voor en ijlt niet na, maar is precies 180 graden in tegenfase met de blauwe lijn.
noot:
het zal je misschien opgevallen zijn dat in deze les het woord "graden" en het teken " ° " door elkaar worden gebruikt.
Dit is expres zo gedaan omdat op examens soms de aanduiding in het woord is en soms in het symbool.
Het betekent precies hetzelfde.