┘
Binair
Je leest binaire getallen van rechts naar links.
Het binaire of tweetallige getalsysteem is een positiestelsel, waarin een getal wordt voorgesteld door een rijtje van de cijfers 0 en 1.
Een dergelijk cijfer wordt in deze context een bit genoemd.
Bijvoorbeeld staat het getal 0110 in het binaire talstelsel voor het getal 6 in het decimale stelsel.
Het eerste getal (rechts dus) staat voor de 1, het tweede getal voor 2, het derde getal voor 4 en het vierde getal voor 8. Nul staat voor afwezig, één staat voor aanwezig.
We zien dat de 1 niet aanwezig is, de 2 is wel aanwezig, de 4 is ook aanwezig en de 8 is niet aanwezig.
Alleen de 2 en de 4 zijn aanwezig, staan aan, en dat staat voor 6 in het decimale stelsel.
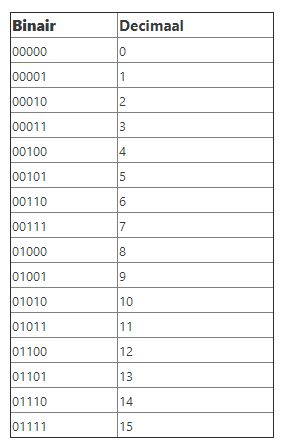
Hierboven zie je een tabel met de cijfers 0 tot en met 15 in decimale notatie en binaire notatie.
Het digitale getal is 5 cijfers lang, dat is 5 bit.
Met 5 bit kunnen we dus 16 verschillende waardes (0 t/m 15) bewerkstelligen.
Met 8 bit zijn dat 256 waardes (0 t/m 255).
Met 16 bit heb je 65536 waardes (0 t/m 65535).
Bij 8 bit hebben wij de bits 0 t/m 7.
Waarom niet van 1 t/m 8 zul je je misschien afvragen.
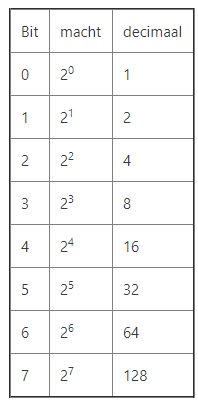
Dit heeft te maken met de exponenten.
De eerste bit staat voor 1, aangeduid met 20 .
Een getal tot de macht nul is altijd 1.
Dit is wiskundig te onderbouwen, maar dat is buiten het bestek van deze cursus.
Het binaire getal 11111111 = 1+2+4+8+16+32+64+128 = 255
Het binaire getal 10101010 = 0+2+0+8+0+32+0+128 = 170
Het binaire getal 01010101 = 1+0+4+0+16+0+64+0 = 85
De 0 betekent dat het bit uitstaat en deze waarde niet voorkomt.
De 1 betekent dat het bit aanstaat en deze waarde wel voorkomt.
We lezen de binaire getallen van rechts naar links
Binaire getallen optellen
Binaire getallen kunnen wij optellen op een vrij eenvoudige manier.
Bij binair optellen gebruik je:
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 10
Voorbeeld:
1010011
1001011
--------------
10011110
Van rechts naar links:
1+1=0 en 1 onthouden
1+1+1=1 en 1 onthouden
1+0+0=1
0+1=1
1+0=1
0+0=0
1+1=0 en 1 onthouden
1=1