┘
Laat je niet afschrikken door onderstaande lesstof, het is waarschijnlijk het moeilijkst te begrijpen onderdeel van de cursus.
Als je het niet helemaal kunt vatten is dit niet erg, als je de vragen van de bijbehorende test goed weet te beantwoorden weet je voldoende.
In de N-cursus werd het digitale signaal behandeld en ook de D.S.P. techniek.
Er bestaan verschillende filters, niet alleen frequentie afhankelijk maar ook analoog of digitaal.
Een analoog filter is meestal opgebouwd uit weerstanden, spoelen en/of condensatoren.
De combinatie van deze componenten bepaalt het gedrag van het filter.
Dat geldt bijvoorbeeld voor een RC (weerstand, condensator) serieschakeling waarbij het signaal over de condensator wordt afgenomen.
Digitale filters maken gebruik van wiskundige formules (algoritmes) en werken alleen op een digitaal signaal.
Een eenvoudig voorbeeld is om het signaal te differentiëren.
Hierbij wordt per sample het verschil met de volgende sample berekend.
Hoge frequenties worden hierbij meer versterkt dan lage.
Door in plaats van het verschil het gemiddelde te nemen van twee opeenvolgende samples, worden juist de hoge frequenties verzwakt.
We gaan hier nu wat dieper op in.
Wanneer we gedigitaliseerde signalen b.v. spraak, willen bewerken kunnen we gebruik maken van digitale filters welke in de D.S.P. techniek veelvuldig gebruikt worden zoals:FIR filters (finite impuls response) is een term die aangeeft dat de impulsresponsie van een (digitaal) filter eindig is.
Een FIR-filter is een computerprogramma dat een filterfunctie uitvoert.
Bij het aanleggen van een puls op een FIR-filter zal het uitgangssignaal na een bepaalde tijd gelijk aan nul worden; de impulsresponsie is dus eindig. In de zuivere vorm berusten ze op een zgn. convolutie berekening.
Zie Convolutie, er is geen terugkoppelterm.
IR-filters zijn, over het algemeen, minder efficiënt dan de hieronder beschreven IIR-filters; ze vereisen meer rekenkracht voor een bepaalde hoeveelheid filtering.
Daarentegen zijn FIR-filters altijd stabiel en gemakkelijk te implementeren.
Bovendien zijn de filtercoëfficiënten relatief eenvoudig te bepalen.
Dit behoort echter niet tot de stof.
FIR-filters komt men zeer vaak tegen in de digitale elektronica om signalen te analyseren en in digitale beeld en geluidsbewerking om ruis uit een afbeelding of audiosignaal te filteren.
Zulke filters kunnen een vlakke fase karakteristiek hebben.
De tegenhanger, het IIR-filter kan dit slechts benaderen.
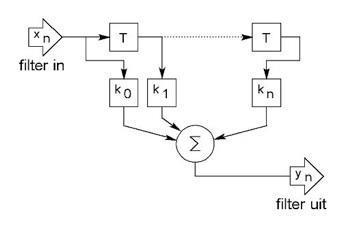
Het figuur rechts geeft een blokschema van een algemeen FIR filter waarin T een (digitaal) vertragingsblok van één bemonstertijd is.
De k's zijn vermenigvuldiging factoren en de sigma S verwerkt de resultaten met behulp van een optelling.
IIR filters:
(infinite impuls response) is een term die aangeeft dat de impulsresponsie van een (digitaal) filter niet eindig is.
Bij het aanleggen van een puls zal het uitgangssignaal van een IIR-filter niet uitdempen, er wordt gebruik gemaakt van terugkoppeling naar de ingang. Het Infinite Impulse Response filter is vooral in de digitale filter techniek bekend, maar eigenlijk zijn ook alle analoge filters van het IIR-type.
Met een IIR filter kan een volstrekt symmetrische impulse responsie (voorwaarde voor een lineaire fase karakteristiek) slechts benaderd worden.
Het uitrekenen van een IIR filter behoort niet tot de stof.
Convolutie
Bij deze digitale technieken wordt de term convolutie vaak gebruikt, hier de uitleg.
Soms heeft de golfvorm en grootte van een signaal alleen onze belangstelling.
Die combinatie zien we in het tijddomein, denk maar aan de grafische voorstelling op een oscilloscoopscherm.
Een andere keer zijn we meer geïnteresseerd in de frequentie, de amplitude en de zijbanden of harmonische van zo'n signaal. (spectrum analyser)
We kijken dan in het frequentiedomein.
Het is mogelijk om, wanneer we een signaal in het tijddomein kennen, uit te rekenen hoe dat signaal er in het frequentiedomein, het frequentiespectrum dus, uit ziet.
Wiskundig heeft Fourier hiertoe al in de 19e eeuw goed werk verricht en we maken nog steeds gebruik van zijn inventiviteit.
Deze omrekening heet dan ook Fourier analyse of Fouriertransformatie.
Bij deze berekening wordt van de bekende golfvorm de spanning punt voor punt vermenigvuldigd met de spanning van een sinusvormig signaal van een bepaalde frequentie.
Alle gevonden uitkomsten worden bij elkaar opgeteld.
De uitkomst geeft aan hoe sterk de frequentie van dit sinusvormig signaal voorkomt in de golfvorm.
Dat punt voor punt vermenigvuldigen heet convolutie en de optelling heet convolutiesom.
Het woord is afgeleid van convolution, wat eigenlijk opgebonden of gebundeld betekent.
Deze convolutiesom moet je bepalen voor alle frequenties waarin je geïnteresseerd bent.
Zo ontstaat een spectrum van het signaal met de gegeven golfvorm.
Nogal een rekenpartij, dus gaan we daar niet al te diep op in, daar zijn processors voor. Fourier gaf ook aan hoe je het omgekeerde kunt doen, dus als je het frequentiespectrum precies kent, hoe je dan de bijbehorende golfvorm kunt uitrekenen, de z.g. inverse Fourier.
Fouriertransformatie
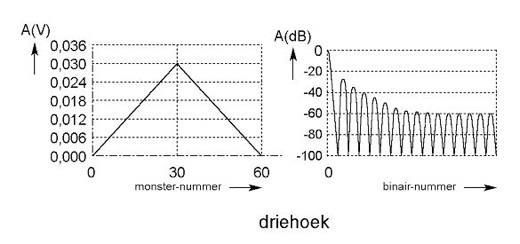
Een voorbeeld van Fouriertransformatie vindt je hier:
De figuren tonen een voorbeeld van een grafische weergave na Fourier transformatie van een triangulair of driehoek functie.
Fourier gaf als wetenschapper vorm aan de wiskunde waarmee fragmenten of segmenten van een signaal van het tijddomein omgezet kunnen worden naar het frequentiedomein.
Wat analoog slechts in heel bepaalde gevallen uit te rekenen was kan met gedigitaliseerde signalen door de computer met 'echte' signalen uitgevoerd worden.
Dat leidt in de DSP techniek (Digitale Signaal Processing techniek) tot (snelle) Fourier - transformatie.
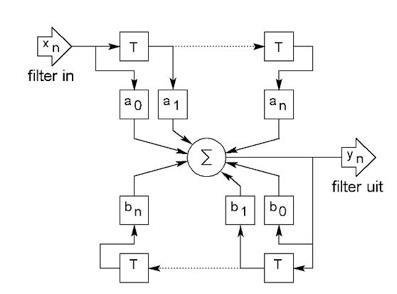
De bovenstaande figuur geeft een blokschema van een algemeen IIR filter waarin T de (digitaal) vertragingsblok van één monstertijd is.0
De a's en de b's zijn vermenigvuldiging factoren en de sigma S verwerkt het (telt alle componenten op).
Je kunt zien dat ten opzichte van het plaatje van de FIR filters er een aantal blokjes zijn bij gekomen:
B0 t/m Bn en de bijbehorende vertragingsblokken.
Deze blokken ontvangen hun input van de uitgang van het filter, en brengen dit weer terug naar de sigma s.
Hierdoor ontstaat nu een lus die tot in het oneindige signaalwaarden " rond pompt ".
Vandaar de naam IIR, Infinite (oneindig) response filter.
Enkele gebruikelijke technieken:
DFT, de afkorting van Discrete (of Digital) Fourier Transform).
Het is een digitale uitvoering van de gebruikelijke Fourier-transformatie en wordt toegepast voor een bemonsterd en gedigitaliseerd signaal.
Het vergt erg veel rekenwerk, maar computers (processors) zien daar niet tegenop.
De normale (langzame) DFT (Discrete Fourier Transform) is een zgn. N-kwadraat-algoritme.
Dat wil zeggen dat je ca. N maal N vermenigvuldigingen moet uitvoeren om een signaal met N samples om te zetten.
FFT is de afkorting van Fast Fourier Transform en vertaald: snelle Fourier - transformatie.
Het is een variant van de Discrete Fourier-transformatie en berekent het spectrum van een bemonsterd signaal op een slimmere, en dus snellere, manier. Het stelt daardoor veel minder hoge eisen aan de beschikbare middelen.
Het FFT-algoritme is vooral bij grotere aantallen inputsamples (ook wel de window size genoemd) veel efficiënter:
FFT is een N*log(N)-algoritme.
Dat wil zeggen dat je slechts N maal de 2-logaritme van N vermenigvuldigingen hoeft uit te voeren.
Rekenen we met 1048 samples van tijdsdomein naar frequentie domein, dan zijn er 1048 x 1048 is ruim een miljoen (orde grootte) vermenigvuldigingen nodig.
Meteen FFT hebben ongeveer 10 x 1048 (ruim 10.000 als ordegrootte) vermenigvuldigingen nodig (dit scheelt een factor 100!).