1.1K - De wetten van Kirchhoff
De 1e wet van Kirchhoff
Als je 5 draadjes in een stervorm aan elkaar knoopt, en je stuurt door 2 draadjes een stroom, dan komt die stroom er via de andere draadjes weer uit. Zijn I1 en I3 ieder 3 ampère, dan zal de uitgaande stroom zich verdelen over I2, I4 en I5, door ieder draadje zal dan 2 ampère vloeien
(I1 en I3 bij elkaar opgeteld en verdeeld over I2, I4 en I5)
Stroom verdwijnt niet zomaar.
Zie de tekening:
De stromen die we insturen ( I1 + I3 ) komen er weer uit, onderverdeeld als I2, I4 en I5.
Hierbij geldt dat I1 + I3 = I2 + I4 + I5
Deze wet van Kirchhoff is dan ook zeker niet ingewikkeld.
Een ander voorbeeld van deze wet is: als je een kruispunt hebt (een 4-sprong), en er komen 20 auto's aan vanaf het Noorden, dan zullen er in totaal ook 20 auto's naar Oost, West en Zuid het kruispunt uitrijden.
Die auto's verdwijnen niet zomaar.
De 2e Wet van Kirchhoff:
Deze is in eerste instantie iets lastiger en abstracter en luidt:
Rondgaande in een schakeling is de som van alle spanningsbronnen en alle spanningsvallen die je daarbij tegenkomt opgeteld gelijk aan nul.
Het volgende voorbeeld illustreert dit:
Stel je staat op een hoogte van 100 meter en je gaat wandelen door een heuvellandschap.
Je gaat hier en daar een aantal meters omhoog (dat hoogteverschil meet je dan even en noteert het) en ergens anders ga je weer omlaag (dat hoogteverschil meet en noteer je ook even).
Als je vervolgens weer terugkomt op je oude plek waar je begonnen bent is dat nog steeds een hoogte van 100m.
Je telt vervolgens alle genoteerde dalingen (negatief) en stijgingen (positief) bij elkaar op.
Je zult daarmee op nul uitkomen.
Zo gaat het ook met spanningen in een elektrisch circuit.
Stel je begint ergens in een circuit en je meet een waarde van 10 volt,
Vervolgens volg je het circuit en noteert alle spanningsstijgingen en alle spanningsdalingen tot je weer terug bent waar je was begonnen; het is daar nog steeds 10 volt.
Alle onderweg gevonden spanning-stijgingen (positief) en dalingen (negatief) zullen bij elkaar opgeteld weer op nul uitkomen.
Ook dit is eigenlijk een heel logische wet.
Toepassingen wet van Kirchhoff:
voorbeeld 1:
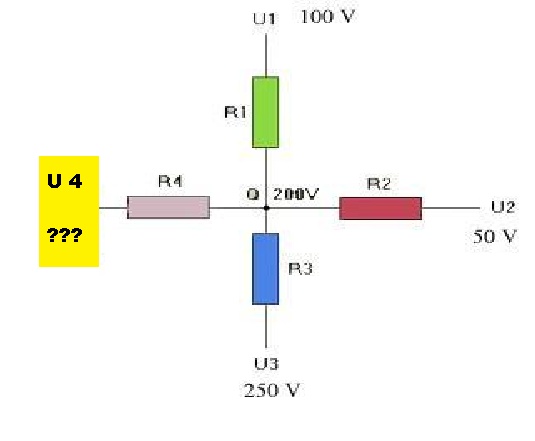
De weerstandwaardes:
R1 = 200 ohm
R2 = 100 ohm
R3 = 700 ohm
R4 = 50 ohm
De spanningen:
U1 = 100 volt
U2 = 50 volt
U3 = 250 volt
U4 = wordt gevraagd
Dit ziet er misschien ingewikkeld uit, echter met de Wet van ohm en een beetje logisch denken met de wetten van Kirchhoff komen we hier eenvoudig uit.
Bijna alle spanningen zijn gegeven, de weerstandswaarden ook, en kunnen we met de wet van ohm de stromen berekenen.
Daar gaat-ie:
•De spanning die over weerstand R1 staat is 100 volt, immers U1 is 100 volt en de spanning in Q, even Uq genoemd, is 200 volt.
•De stroom door R1 bedraagt dan 100200100200 = 0,5 ampère.
•Deze stroom (die we I1 noemen) loopt van Q naar U1, in de tekening dus omhoog.
•Op dezelfde manier zien we dat over R2 een spanning staat van 150 volt
•De stroom door R2 bedraagt: 150100150100= 1,5 ampère.
•Deze stroom (noemen we I2) loopt van Q naar U2 (dus naar rechts in de tekening) omdat Uq hoger is dan U2.
•Over R3 staat een spanning 50 volt.
•Dus door R3 loopt de volgende stroom I3 = 5070050700 = 0,071 ampère.
•Deze stroom loopt van U3 naar punt Q toe.
•U4 weten we dus niet maar we weten wel dat er de uitgaande stromen vanuit Q zijn: I1 + I2 = 0,5 + 1,5 = 2 ampère.
•Die stroom komt wel ergens vandaan, dus vanuit U3 (dat was I3 = 0,071 ampère) en de rest vanuit U4.
•U4 moet dus 2 - 0,071 = 1,93 ampère leveren.
•Dan loopt er totaal 2 ampère naar punt Q toe via R3 en R4 en er gaat ook weer 2 ampère uit via R1 en R2.
•Met de wet van ohm kunnen we nu U4 uitrekenen:
•I4 (stroom door R4) = 1,93 ampère , R4 = 50 ohm, de spanning over R4 moet zijn 1,93 x 50 = 96,5 volt.
•Deze 96,5 volt moet dusdanig staan dat de stroom naar Q gaat dus de spanning U4 zal 200 + 96,5 volt zijn om dit voor elkaar te krijgen.
Wat hebben we zojuist toegepast:
•Wet van ohm, die is helder.
•De stromen in Q met elkaar in verband brengen: 1e wet van Kirchhoff
•Spanningen in een keten bij elkaar optellen om zo U4 te krijgen: 2e wet van Kirchhoff.
Voorbeeld
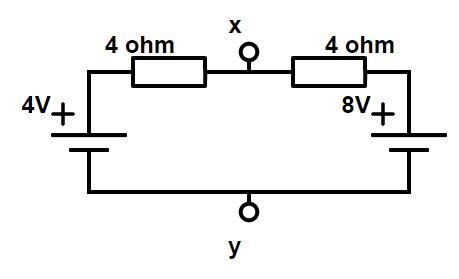
Zie de bovenstaand figuur.
De vraag is: Wat is de spanning tussen X en Y.
Dit ziet er in eerste instantie een beetje raar uit.
Er zijn 2 spanningsbronnen in dit circuitje en die staan nog tegen elkaar in ook.
Is dit moeilijk?
Welnee!
Er is een batterij van 8 volt en er staat er een van 4 volt tegenin.
We houden dus 4 volt over om de stroom in het rondje te sturen.
Totaal zit er 8 ohm in het circuit dus er loopt een stroom van 4 volt / 8 ohm = 0,5 ampère tegen de wijzers van de klok in.
De spanningsval over iedere weerstand is volgens de wet van ohm 0,5 x 4 = 2 volt.
De stroom loopt zoals gezegd tegen de wijzers van de klok in dus de polariteit van de spanning over de weerstanden is zo dat de plus aan de rechterkant in de tekening zit.
Doen we nu even een 2e wet van Kirchhoff trucje.
We beginnen in Y, dat noem ik even het relatieve 0-punt.
We gaan tegen de wijzers van de klok door het circuit heen.
Na de 8 volt bron zit je 8 volt boven de waarde van Y, in punt X verlies je dan 2 volt door de weerstand van 4 ohm en sta je op 6 volt.
Na de linker weerstand verlies je weer 2 volt en sta je op 4 volt om vervolgens met de bron van 4 volt weer 4 volt te zakken naar je relatieve nulpunt Y.
Dit vertoont erg grote gelijkenis met het voorbeeld in het vorige hoofdstukje waar we over een paar heuvels wandelden.
Als we de relatieve 0-waarde van Y even 0 volt denken, dan komt X dus uit op 0 volt + 8 volt
(de bron) - 2 volt (spanningsval weerstand) = 6 volt.
En dat is het antwoord op de gestelde vraag.
Wat hebben we hier toegepast:
•2e wet van Kirchhoff
•Wet van ohm
•Logisch denken
Beide typen vraagstukken komen regelmatig voor op het examen. Mocht je nog twijfels hebben of je deze nu kunt oplossen, overleg dan met een van de cursistenbegeleiders en maak wat vraagstukken. Vergeet in ieder geval nooit logisch na te denken en laat je niet afschrikken door een ingewikkelde tekening.


┘
┘




